Trigonometry (from Greek trigōnon "triangle" + metron "measure")[1] is a branch of mathematics that studies triangles, particularlyright triangles. Trigonometry deals with relationships between the sides and the angles of triangles and with the trigonometric functions, which describe those relationships, as well as describing angles in general and the motion of waves such as sound and light waves.
Pre-Hellenic societies such as the ancient Egyptians and Babylonians lacked the concept of an angle measure, but they studied the ratios of the sides of similar triangles and discovered some properties of these ratios. Ancient Greek mathematicians such asEuclid and Archimedes studied the properties of the chord of an angle and proved theorems that are equivalent to modern trigonometric formulae, although they presented them geometrically rather than algebraically. The sine function in its modern form was first defined in the Surya Siddhanta and its properties were further documented by the 5th century Indian mathematician and astronomer Aryabhata.[2] These Indian works were translated and expanded by medieval Islamic scholars. By the10th century Islamic mathematicians were using all six trigonometric functions, had tabulated their values, and were applying them to problems in spherical geometry. At about the same time, Chinese mathematicians developed trigonometry independently, although it was not a major field of study for them. Knowledge of trigonometric functions and methods reached Europe via Latin translations of the works of Persian and Arabic astronomers such as Al Battani and Nasir al-Din al-Tusi.[3] One of the earliest works on trigonometry by a European mathematician is De Triangulis by the 15th century German mathematician Regiomontanus. Trigonometry was still so little known in 16th century Europe that Nicolaus Copernicus devoted two chapters ofDe revolutionibus orbium coelestium to explaining its basic concepts.




The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below underMnemonics).



Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.
Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan and sometimes cis) and their inverses. Most allow a choice of angle measurement methods: degrees, radians and, sometimes, grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built-in instructions for calculating trigonometric functions.
Applications of trigonometry
There are an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
Fields which make use of trigonometry or trigonometric functions include astronomy (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology,medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, landsurveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.
Common formulae
The law of sines (also known as the "sine rule") for an arbitrary triangle states:
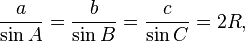
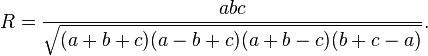
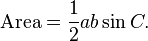
The Law of Cosines
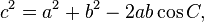

The Law of Tangents
Welcome to Official Megan's Website
Halaman
Trigonometry
Trigonometry is usually taught in secondary schools either as a separate course or as part of a precalculus course. It has applications in both pure mathematics and in applied mathematics, where it is essential in many branches of science and technology. A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomyand navigation.
All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O.
History
Overview
In this right triangle: sin A = a/c, cos A = b/c, tan A = a/b.
If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functionsof the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:
The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec) and cotangent (cot), respectively. The inverse functions are called the arcsine, arccosine, andarctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities.
With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and an angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since everypolygon may be described as a finite combination of triangles.
Sine function drawing process
Tangent function drawing process
Cosec drawing process
Graphs of the functions sin (x) and cos (x), where the angle x is measure in radians
The Law of Sines
where R is the radius of the circumcircle of the triangle:
Another law involving sines can be used to calculate the area of a triangle. If you know two sides and the angle between the sides, the area of the triangle becomes:
The law of cosines ( known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
or equivalently:
Source : Wikipedia
Langganan:
Posting Komentar (Atom)
Blog Archive
About Me

- Yoga Fitrah Annurrahman
- Hai guys, let me introduce my self. My name is Yoga Fitrah Annurrahman, you can call me as Yoga. I love everything about science, animation, and so on. But, i hate liar, and everything that's sucks. So, i'm just ordinary person.
Followers
Wp Theme by Promiseringsdesigns | Blogger Template by Anshul
![\frac{a-b}{a+b}=\frac{\tan\left[\tfrac{1}{2}(A-B)\right]}{\tan\left[\tfrac{1}{2}(A+B)\right]}](http://upload.wikimedia.org/math/c/b/5/cb5c755b587d4e4e1f4367c492c4de8d.png)

Tidak ada komentar:
Posting Komentar